![]()
Tout point M de la droite (AB) convient, l’angle correspondant est nul. Supposons donc qu’il existe un point M du plan solution au problème posé et n’appartenant pas à (AB).
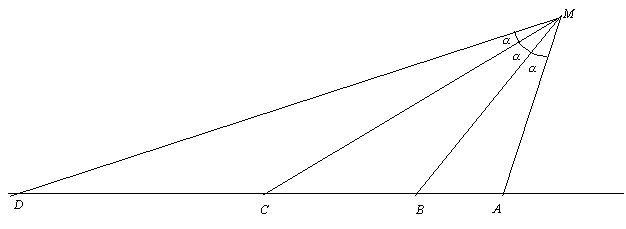
(MC) est bissectrice de l’angle ![]() et (MB) est bissectrice de l’angle
et (MB) est bissectrice de l’angle ![]() .
Il s’agit donc de traduire ces deux propriétés ou bien géométriquement
ou bien analytiquement.
.
Il s’agit donc de traduire ces deux propriétés ou bien géométriquement
ou bien analytiquement.
Soit ABC
un triangle. Si la bissectrice intérieure de l’angle A coupe [BC] en G,
alors ![]() .
.
Ce résultat peut-être obtenu au moins par deux méthodes simples :
|
Par des considérations d’aires :
G est équidistant des deux côtés [AB]
et [AC] . Soit k cette
distance commune et soit H le projeté
orthogonal de A sur [BC]. L’aire du triangle ABG
est
| |
|
Par des considérations trigonométriques :
Appelons a
la valeur commune des angles définis par la bissectrice (AG) et b
l’angle BGA . Dans le triangle ABG, |
Revenons
maintenant au problème posé et appliquons le lemme dans les triangles MAC et MBD. Comme
AB = 1, BC
= 2 et CD
= d, on obtient les deux relations :
![]() .
.
Les points M cherchés
sont donc tels que :
4MA2
– MC2 =0
et d2
MB2 – 4 MD2 = 0.
(1)
Ces expressions sont équivalentes à :
![]() .
.
Le barycentre du système {(A,2);(C,1)}est le point B, celui
de {(A,2) ;(C,-1)}
est
le symétrique B’ de C par rapport à A.
![]() signifie que M
appartient au cercle G1
de diamètre [BB’].
signifie que M
appartient au cercle G1
de diamètre [BB’].
Le barycentre du système {(B,d) ;(D,2)}
est le point C et lorsque d¹ 2,
celui de {(B,d) ;(D,-2)}
est le point C’ tel que ![]() .
.
![]() signifie que M appartient
au cercle G2
de
diamètre [CC’].
signifie que M appartient
au cercle G2
de
diamètre [CC’].
Pour que les deux cercles se coupent il
faut et il suffit que C’
appartienne au segment [BB’]. Donc
que d’une part d>2 et d’autre
part que ![]() ce qui
entraîne d
³
6.
ce qui
entraîne d
³
6.
Le cas d=2 place M sur la médiatrice de [BD] qui ne coupe pas le cercle G1 .
L’énoncé du problème laisse supposer que l’on recherche des solutions dans un demi plan limité par la droite (AB). Il existe donc une seule solution n’appartenant pas à cette droite lorsque d >6.
Remarque : On peut également montrer que C’ est le barycentre du système {(B,d-6) ; (B’,d+2)} et l’on retrouve bien que C’ appartient au segment [BB’] si et seulement si d ³ 6.
![]()
Reprenons
les relations (1) : 4MA2
– MC2 =0 et d2
MB2 – 4 MD2 = 0
et interprétons les en utilisant un repère orthonormal du plan, par
exemple le repère ![]() . Les points A, B, C, D, M ont
respectivement dans ce repère les coordonnées : (3,0) ; (2,0) ;
(0,0) ; (-d,0) et (x,y) . Nous pouvons même supposer y > 0.
. Les points A, B, C, D, M ont
respectivement dans ce repère les coordonnées : (3,0) ; (2,0) ;
(0,0) ; (-d,0) et (x,y) . Nous pouvons même supposer y > 0.
4MA2
– MC2 = 0 s’écrit : ![]() soit
soit
![]() . Le point M appartient donc au cercle G1 de centre
W1 (4,0) et
de rayon 2. Il
s’agit bien du cercle de diamètre [BB’]
où B’(6,0).
. Le point M appartient donc au cercle G1 de centre
W1 (4,0) et
de rayon 2. Il
s’agit bien du cercle de diamètre [BB’]
où B’(6,0).
d2
MB2 – 4 MD2 = 0 s’écrit :
![]() . Le cas d = 2
ne fournissant aucune solution, l’expression précédente devient après réduction :
. Le cas d = 2
ne fournissant aucune solution, l’expression précédente devient après réduction : ![]() . M
appartient donc au cercle G2 de centre
W2
. M
appartient donc au cercle G2 de centre
W2 ![]() . Ce cercle passe par C . Une
condition nécessaire pour qu’il recoupe G1
est
que l’abscisse de son centre soit positive. Il est donc nécessaire que d
>2. Dans ces conditions, l’abscisse du point C’
, diamétralement opposé à C est
donc
. Ce cercle passe par C . Une
condition nécessaire pour qu’il recoupe G1
est
que l’abscisse de son centre soit positive. Il est donc nécessaire que d
>2. Dans ces conditions, l’abscisse du point C’
, diamétralement opposé à C est
donc
![]() et l’on doit avoir
et l’on doit avoir
![]() £
6, ce qui
permet bien de retrouver la condition d ³
6. Remarquons que d = 6 redonne M = B’
et que d = 10 donne M (4,2). Ce
point est «au dessus» de W1
, c’est le point solution le plus éloigné de (AB).
£
6, ce qui
permet bien de retrouver la condition d ³
6. Remarquons que d = 6 redonne M = B’
et que d = 10 donne M (4,2). Ce
point est «au dessus» de W1
, c’est le point solution le plus éloigné de (AB).
![]()
A, B, C étant trois points du plan, repérés
dans un repère orthonormal, on a
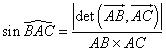
Appliquons cela dans le cas de la figure et dans le même repère que précédemment.
On obtient la double égalité :
![]() .
.
On obtient successivement :
![]() ce qui fournit les deux relations
ce qui fournit les deux relations ![]() en supposant y > 0.
en supposant y > 0.
On se retrouve donc dans le cadre de la solution 2.
Remarque :
l’écriture de l’égalité des cosinus conduit à des calculs beaucoup plus
complexes qui aboutissent néanmoins.
![]()
![]()