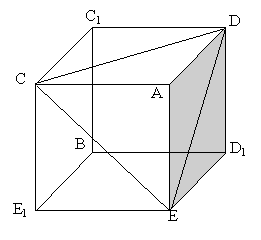
Les deux cubes ayant une diagonale commune sont isométriques et se déduisent l’un de l’autre par rotation autour de la diagonale commune (AB). L’idée est donc de projeter les six sommets de ces deux cubes, autres que A et B sur un plan orthogonal à (AB), par exemple, le plan P médiateur de (AB). Nommons les sommets du cube c comme indiqué sur la figure 1 ci dessous et ceux du cube c’ avec les mêmes lettres “primées”. Les points C, D, E, C’, D’, E’ d’une part et C1, D1, E1, C’1, D’1, E’1 d’autre part appartiennent à deux cercles de même axe (AB). Toutes les arêtes des deux cubes font le même angle avec le plan P .
(Cet
angle 
est
d’ailleurs défini par son cosinus : ,
calculé par exemple dans le tétraèdre ACDE )
Il en résulte que les longueurs des projections orthogonales de ces arêtes sur P sont toutes égales. Les projetés orthogonaux sur P des points C, D, E, C1, D1, E1 d’une part et C’, D’, E’, C’1, D’1, E’1 d’autre part sont donc disposés aux sommets de deux hexagones réguliers dont l’un est l’image de l’autre par une rotation d’angle donné. Nommons ces projetés orthogonaux avec les mêmes lettres en minuscule. On obtient la figure 2.
 |
 |
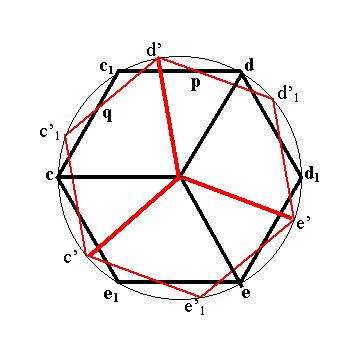Figure 1 |
Figure 2 |
 |
 |
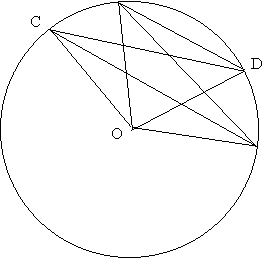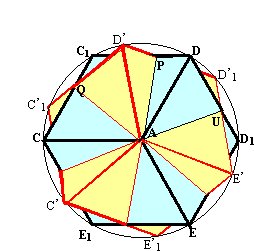
Figure 3 |
Figure 4 |
 |
a-
Soient [AB] et [CD] sont deux cordes de même longueur, alors les droites (AD)
et (BC) sont parallèles. C’est un bon exercice d’application des
cas d’égalité des triangles en seconde. En cette année de première, le
résultat est obtenu par égalité des angles au centre associés aux deux
cordes puis à celle des arcs CA et DB les angles
inscrits font le reste. (figure 4) |
|
b- Soient (d) une droite d’un plan (P) et (d’) une droite d’un plan (P’) parallèle à (P). Soit (d1) la projetée orthogonale de (d’) sur (P). Si (d1) est parallèle à (d) alors (d) est parallèle à (d’). En effet, les plans (P) et (P’) étant parallèles, les droites (d’) et (d1) sont parallèles d’où le résultat par transitivité du parallélisme. |
Revenons à la figure 2 et intéressons nous à la configuration dd’c1d’1 . d’après le résultat établi en a), les droites (dd’) et (c1d’1) sont parallèles et sont les projetées orthogonales des droites (DD’) et (C1D’1) situées dans des plans parallèles. Les droites (DD’) et (C1D’1) sont donc parallèles donc coplanaires. Les segments [DC1] et [D’D’1] sont donc sécants en un point P dont le projeté orthogonal sur P est noté p. On détermine ainsi six points P, Q, R, S, T, U de projetés p, q, r, s, t, u. Les rotations conservant les rapports de distances, les points p et q partagent les segments [C1D] et [CC1] dans le même rapport comme d’ailleurs les points r, s, t, u sur leurs segments respectifs. Il en est donc de même pour les points P, Q, R, S, T, U sur leurs arêtes respectives puisque toutes les arêtes du cube c font le même angle avec le plan P. La figure 3 donne la construction des 6 points déterminés.
Le
volume commun aux deux cubes est obtenu en retirant au volume du cube c, les
volumes de six tétraèdres isométriques du
type PAUD. Appelons l
la longueur de l’arête du cube et x
la longueur UD. Le volume du cube c est l3
et le volume du tétraèdre PAUD est 
.
On obtient donc le volume V(x) cherché :
On
déduit enfin de cette formule que et
que cette valeur est obtenue pour x =l/2. Pour cette valeur
de x, les points P,
Q,
R,
S,
T,
U sont confondus avec leurs projetés orthogonaux sur P :
p,
q,
r,
s,
t,
u.
