Problèmes de constructions et de lieux géométriques

Cercles tangents à un cercle et une droite

Objectif, niveau et difficultés
Ce problème est constitué de deux parties. Dans un premier temps, il s’agit de construire un cercle tangent à un cercle donné et à une droite donnée qui ne coupe pas ce cercle. Il y a une double infinité de solutions, selon que le cercle construit est tangent extérieurement (partie I) ou intérieurement (partie III) au premier cercle. L’objectif est ensuite de voir s’il y a un ordre particulier dans tous ces cercles ainsi construits, plus précisément en déterminant le lieu géométrique de leurs centres (on trouve deux paraboles). Le problème est riche, il doit comporter une partie expérimentale avec un logiciel de géométrie dynamique (partie II, question 1). Il peut être abordé en 1^ère S ou Terminale S.

On se donne un cercle c de centre A et de rayon , et une droite d ne coupant pas le cercle c.

	Dans la Partie I de ce problème, on construit un cercle Г vérifiant la condition : (p) : « Г est tangent à la fois à c et d, le cercle c étant à l’extérieur de Г ».
	Dans la Partie II, on étudie le lieu géométrique des centres Ώ de tous les cercles Г vérifiant cette condition.
	Dans la Partie III, on généralise le problème en étudiant le cas où c est intérieur à Г.

Partie I

On considère un point M de d, et on s’intéresse au cercle Г vérifiant la condition (p), et tangent à la droite d en M.

Justifier que le centre Ώ de Г se trouve sur la droite Δ, perpendiculaire à d en M.
On note H le point d’intersection du cercle c et du segment [ΏA].
1. Justifier que le point Ώ est équidistant des points M et H.
2. En déduire une relation entre les distances ΏM et ΏA.
3. Conclure en en indiquant une construction du point Ώ et du cercle Г
  (on pourra utiliser une droite d’, parallèle à d et telle que la distance de d à d’ égale r).

Partie II

Dans cette partie, on munit le plan d’un repère orthonormal .
On considère que la droite d est l’axe (Ox), et que le point A, centre du cercle c, a pour coordonnées (O ; a)
(a réel strictement supérieur à r).

1. En utilisant un logiciel de géométrie dynamique, construire la figure étudiée en Partie I.
2. Conjecturer le lieu géométrique du centre Ώ de Г lorsque le point M décrit la droite d.
Démontrer cette conjecture en exprimant les coordonnées du point Ώ en fonction de l’abscisse du point M.

Variante pour la question 2

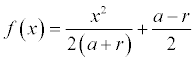Démontrer cette conjecture en vérifiant que, lorsque M décrit D, le point Ώ décrit la courbe représentative de la fonction f définie sur R par .

Note :
On obtient une figure analogue à la figure ci-dessous.

Partie III

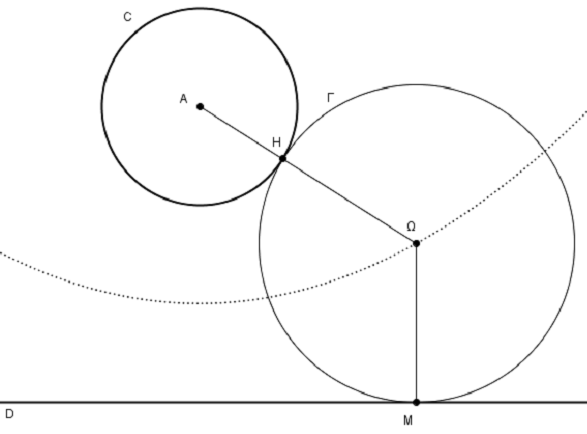
Reprendre la Partie II en considérant désormais la condition :
(p’) : « Г est tangent à la fois à c et à d, le cercle c étant à l’intérieur de Г ».