![]()
| Première question |
[BA] étant un diamètre de c1, le triangle BMA est rectangle en M. Les droites (BM) et (AM’ ) sont donc parallèles. c2 est l’image de c1 par deux homothéties. L’une, de rapport négatif a pour centre A et l’autre, de rapport positif envoie B sur A. Notons h cette seconde homothétie. h(M) est un point N de c2 tel que (BM ) et (AN ) soient parallèles. On a donc bien N = M’ puisque par hypothèse, les points A, M, M’ sont distincts. (MM’ ) passe donc par le centre O de l’homothétie h ; c’est un point fixe de la droite (O1O2).
![]()
| Deuxième question |
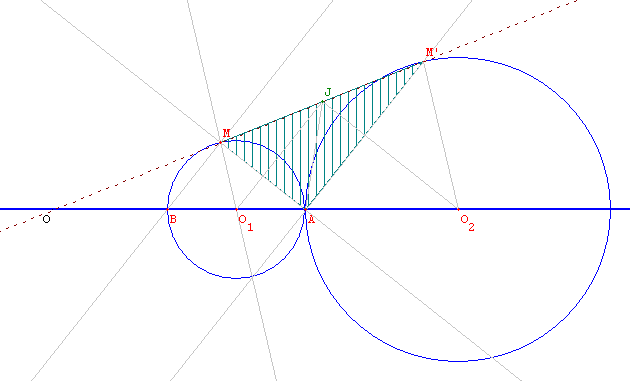
(O1J ) est médiatrice de [AM], (O2J )
est médiatrice de [AM’ ]. Le triangle O1JO2
est rectangle en J . J appartient donc au cercle de diamètre
[O1O2].
Réciproquement, soit J un
point du cercle de diamètre [O1O2]. Lorsque
J est distinct de O1 et de O2, les
perpendiculaires issues de J à (O1J ) et à (O2J )
recoupent c1 et c2
en M et M’ . Comme
O1M = O1A et
que O2M’ = O2A, (O1J)
et (O2J) sont les médiatrices respectives des
segments [AM] et [AM’ ]. Le triangle MAM’ est
bien rectangle en A. L’ensemble
cherché est le cercle de diamètre [O1O2]
privé des points O1 et O2.
![]()
| Troisième question |
Posons :
|
|
|
|
L’aire du triangle MAM’ est donc a(x)=
![]() . Cette expression est maximale lorsque x=p/2
. Cette expression est maximale lorsque x=p/2
![]()
Remarques :
|
![]()
![]()
|
Télécharger un corrigé au format PDF compressé
Télécharger les figures Géoplan Geospace
|
![]()