Exercice n°2 : corrigé

1. Le cas « 1,5 ».

Supposons que AB=x. On a donc AC = AD = BC = BD = CD = y.
Les triangles ACD et BCD sont équilatéraux.
On obtient une seule configuration puisque A ¹ B. (fig1).

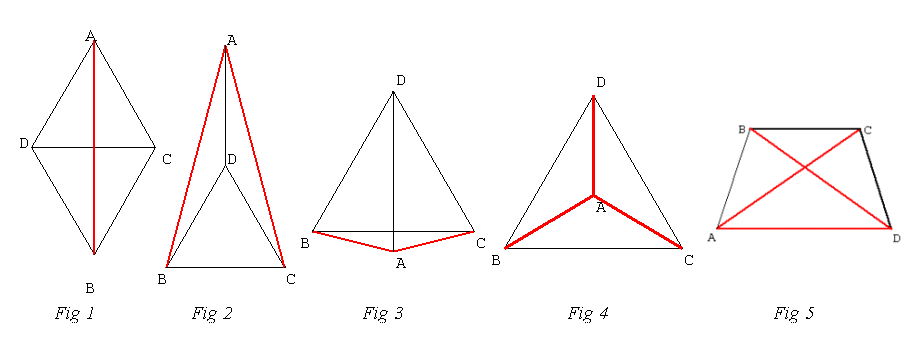
2. Le cas « 2,4 ».
   

1. Posons AB=CD =x.
   On a donc AC, AD, BC, BD=y.
   Le quadrilatère cherché est un losange dont les diagonales ont même longueur, c’est le carré donné en exemple.
   

2. Posons AB=AC=x.
   On a donc AD, BC, BD, CD=y.
   Le triangle BCD est équilatéral, A est à l’intersection de la médiatrice de [BC] et du cercle de centre D et de rayon y.
   On a donc deux configurations : fig2 et fig3 .
   

3. Le cas « 3 ,3 ».
   

1. Les trois segments de longueur x sont disposés en étoile, par exemple AB=AC=AD=x.
   On a donc BC=BD=CD=y.
   Le triangle BCD est équilatéral et A est le centre de ce triangle : fig4.
   

2. Si les trois segments de longueur x forment un triangle équilatéral, on retrouve la précédente configuration.
   

3. Il reste le cas où les trois segments de longueur x forment une chaîne ouverte . Posons AB=BC=CD=x.
   On a donc AC=AD=BD=y.
   Les triangles BDA, ADC, ABC et BCD sont isocèles.
   Appelons O le point d’intersection des segments [BD] et [AC].
   Les triangles BDA et ADC d’une part , ABC et BCD d’autre part sont isométriques (3ème cas).
   Les angles CAD et BAD d’une part, DBC et ACB d’autre part sont égaux . Puisque les angles BOC et AOB sont opposés par le sommet, ils sont égaux ce qui entraîne l’égalité des quatre angles précédents et le parallélisme des droites (BC) et (AD). La configuration cherchée est un trapèze isocèle : fig5.