![]()
Dans le cas général, appelons a l’angle
et b l’angle
puisque (RT) est la médiatrice de [AS]. Évaluons donc tanb de deux manières. Dans le triangle RTA d’une part et dans le triangle SAB d’autre part. On obtient ainsi
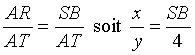
Dans le cas particulier où T = D, on a y = 6 et d’après le théorème de Pythagore,
.
On obtient ainsi la valeur minimale.
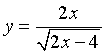
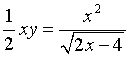 . Appelons f
cette fonction, elle est dérivable sur l’intervalle
. Appelons f
cette fonction, elle est dérivable sur l’intervalle
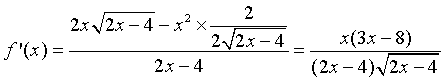
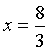 .
.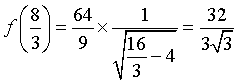 .
.
Notons que dans ce cas,
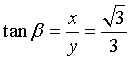 ce qui
signifie que le triangle RST est équilatéral.
ce qui
signifie que le triangle RST est équilatéral.
![]()
|
Télécharger un corrigé au format PDF
|
![]()