![]()
 |
 |
Objectifs : Le but de ce problème est d’étudier une suite définie par récurrence (question 2), de mettre en évidence que cette suite est périodique lorsque son premier terme est rationnel (question 2), puis de démontrer ce résultat (question 3). Dans les questions 4 et 5, on envisage la réciproque de cette propriété, dont la démonstration repose sur certains résultats préliminaires établis dans la question 1.
Niveau et difficultés : Les outils
utilisés sont les fonctions affines, la notion de composée, les suites définies
par récurrence, la notion de nombre rationnel. Le problème est donc abordable en
1ère S.
L’usage d’un tableur est recommandé.
Certaines questions font appel au programme de Terminale,
comme la notion de fonction continue en 1.d), le raisonnement par récurrence en
1.e), 3.c) ou 4.d). Ces difficultés peuvent être contournées en se contentant de
l’idée du raisonnement.
Les questions 1.d) et 1.e), qui sont techniquement plus
difficiles, peuvent être admises.
![]()
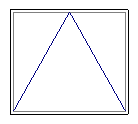
La fonction « chapeau de clown » f est définie sur [0,
1] par : 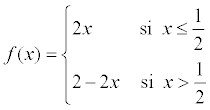 .
.
Montrer que pour tout x de [0, 1], on a :f(x) € [0, 1], et
représenter graphiquement la fonction f.
(La fonction doit son nom à la forme de
sa représentation graphique.)
Donner une expression de la fonction
![]() sur chacun des quatre
intervalles
sur chacun des quatre
intervalles 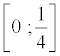 ,
,
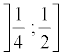 ,
,
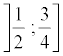 ,
,
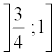 , puis représenter graphiquement la fonction
, puis représenter graphiquement la fonction
![]() .
.
Plus généralement, on note
![]() ,
,
![]() et, pour tout
p ≥ 1 :
et, pour tout
p ≥ 1 :![]() .
.
(Ainsi, fp est
la composée de f par elle-même, et ce, p fois.)
|
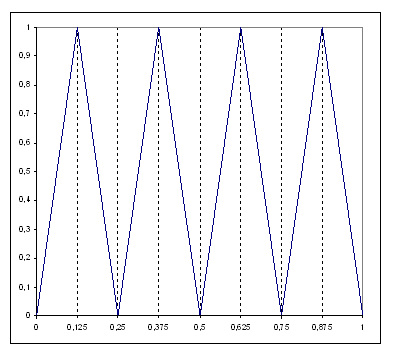
Vérifier que la figure ci-contre est la représentation
graphique de la fonction f3. |
 |
Soit p un entier naturel non nul.
Montrer que fp est continue
sur [0 ; 1] et que pour tout entier naturel m compris entre 0 et 2p ,
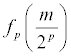 est égal à 0
si m est pair, et à 1 si m est impair.
est égal à 0
si m est pair, et à 1 si m est impair.
Soit p un entier naturel non nul.
Montrer, par récurrence
sur l’entier p, que pour tout entier m compris entre 0 et 2p - 1, la restriction de
la fonction fp à l’intervalle
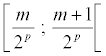 est une fonction affine à coefficients entiers.
est une fonction affine à coefficients entiers.
(Autrement dit, il s’agit de prouver qu’il existe deux
entiers naturels ap,m et bp,m tels que l’on ait, pour tout réel x de l’intervalle
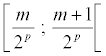 :
:
![]() .
.
Pour
établir la propriété au rang p + 1, on pourra remarquer que fp + 1(x) est égal soit à
fp(2x) soit à fp(2-2x).)
![]()
On appelle suite « chapeau de clown » une suite (un) dont le premier terme u0 appartient à [0 ; 1] et qui vérifie, pour tout entier n : un + 1 = f(un).
Quelle est la suite « chapeau de clown » correspondant à u0 = 0 ?
Quelle est celle correspondant à u0 = 1 ? à
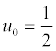 ?
?
Lorsque
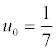 , utiliser 1.a) pour
représenter graphiquement les termes de la suite.
, utiliser 1.a) pour
représenter graphiquement les termes de la suite.
Vérifier que la suite est
périodique et préciser sa période.
Dans chacun des cas suivants, vérifier que
la suite obtenue est encore périodique et déterminer sa période :
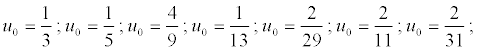
(On pourra utiliser un tableur, en mettant les cellules au format
fractionnaire.)
Soit k un entier fixé (k ≥ 1 ).
Écrire la liste de toutes les
valeurs de la suite pour
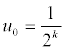 .
.
De même pour 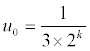 .
.
Peut-on déterminer u0 de façon à
obtenir une suite périodique de période 4 ?
Une suite périodique de période k (k
étant un entier naturel quelconque) ?
![]()
On suppose dans cette question que u0
est rationnel, c’est-à-dire que u0 peut s’écrire sous la forme
d’une fraction ![]() ,
avec a et b entiers naturels.
,
avec a et b entiers naturels.
Montrer que tous les termes de la suite « chapeau de clown
» correspondante sont rationnels.
Que peut-on dire de leurs dénominateurs ?
Montrer qu’il y a dans la suite (un) au moins deux termes égaux.
En déduire qu’à
partir d’un certain rang la suite est périodique, de période inférieure ou égale
à ![]() .
.
Peut-on avoir une période égale à
![]() ?
?
![]()
On suppose que (un) est rationnel pour un entier n supérieur ou égal à 1.
Quelles sont les valeurs possibles de un - 1 ?
En déduire que un - 1 est
rationnel.
Montrer alors que tous les termes de la suite sont rationnels.
Si u0 est irrationnel, que peut-on dire de tous les termes de la suite ?
![]()
On suppose dans cette question que la suite est périodique de période p ( p ≥ 1 ), à partir du rang k, c’est-à-dire que pour tout entier naturel n ≥ k, on a : un + p = un.
Montrer que uk = fp(uk), la fonction
fp étant celle définie en 1.b).
En déduire que uk est un nombre rationnel.
À l’aide des questions précédentes, donner une condition nécessaire et suffisante portant sur le premier terme pour qu’une suite « chapeau de clown » soit périodique.
![]()