Nombres réels et Analyse
Suites - Thème N°7
La conjecture de Syracuse

    Objectif : Ce thème propose de se confronter à un problème non résolu, dont l’énoncé est très simple, et qui tient les mathématiciens en échec depuis une cinquantaine d’années. Il s’agit, de façon très élémentaire, d’engager quelques essais d’avancée vers la solution, grâce surtout à l’informatique et à un peu de raisonnement.
    L’usage d’un tableur est fortement recommandé ; la définition de la suite demande d’utiliser une formule comportant une instruction conditionnelle.

    Niveau et difficultés : La première partie peut être abordée en 1^ère S, car elle ne requiert que la définition d’une suite par récurrence. La deuxième partie met en jeu la notion de congruence ; elle sera réservée aux élèves de Terminale S suivant l’enseignement de spécialité.

    Une suite (u_n) de Syracuse est définie par la donnée de son premier terme u₀, entier naturel non nul, et pour tout entier naturel n, par la relation de récurrence :
    si u_n est pair, alors 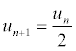, sinon u_n + 1 = 3u_n + 1.

    Tester le comportement d’une suite de Syracuse pour diverses valeurs de l’entier de départ u₀.
    Il est recommandé d’utiliser un tableur, ou un programme sur calculatrice, ou un logiciel de calcul formel.

    On constate que, quel que soit l’entier de départ u₀, on aboutit toujours à la période 4, 2, 1.
    Cette propriété constitue la conjecture de Syracuse, que l’on peut formuler ainsi :
    Soit (u_n) une suite de Syracuse. Il existe un entier p tel que u_p = 1.

    La démonstration de cette conjecture résiste depuis plus de 50 ans aux mathématiciens du monde entier. Son nom provient de l’université de Syracuse (état de New-York, Etats-Unis) où elle a été étudiée dans les années 1950.

 A - Un peu de vocabulaire sur les suites de Syracuse

    Les définitions suivantes ne sont pertinentes que si la conjecture de Syracuse est vérifiée, ce qui n’est pas prouvé pour l’instant.

    Soit n un entier naturel non nul.
    On appelle vol numéro n la liste des termes de la suite de Syracuse (u_n) depuis l’entier de départ jusqu’au premier 1.
    Par exemple, le vol numéro 13 est égal à :
    13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

    La durée du vol d(n) d’un entier n est le nombre d’étapes nécessaires pour atteindre le premier 1 depuis u₀ = n.
    C’est le plus petit indice p tel que u_p = 1.
    Par exemple d(13) = 9.

1. Calculer les durées de vol des nombres 26 et 27.
    

2. Soit δ un entier naturel non nul.
   Existe-t-il un entier dont la durée de vol est δ ?
    

    L’altitude maximale am(n) d’un entier n est le plus grand entier de son vol.
    Par exemple : am(13) = 40.

3. Déterminer les altitudes maximales des entiers 26 et 27.

    Un entier n a un vol de durée record si sa durée n’est jamais atteinte par les entiers inférieurs :
   .

4. Vérifier que 27 a un vol de durée record et déterminer le record suivant.

    Un entier n a un vol d’altitude maximale record si son altitude maximale n’est jamais atteinte par les entiers inférieurs :
   .

5. Vérifier que 27 a un vol d’altitude maximale record et déterminer le record suivant.

B - Vérifications de la conjecture de Syracuse

    Faute de démontrer la conjecture de Syracuse, les mathématiciens l’ont vérifiée par programme informatique pour des valeurs de 1 à N. Actuellement N est supérieur à 10¹⁶ et aucun contre-exemple n’a été trouvé. On étudie dans cette partie quelques astuces pour diminuer le nombre de vérifications nécessaires.
    En effet, si nous effectuons la vérification de la conjecture successivement pour les entiers de 1 à N, il est inutile de poursuivre le calcul du vol numéro n dès qu’un terme de la suite est strictement inférieur à n.
    Par exemple, il est inutile de vérifier la conjecture pour les entiers pairs puisque, dès la première étape :
    .

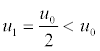1. Démontrer qu’il est inutile de vérifier la conjecture pour les entiers congrus à 0, 1 ou 2 modulo 4.
    

2. Il reste donc à vérifier la conjecture pour les entiers congrus à 3 modulo 4.
   Quel peut être le reste d’un tel entier dans la division par 8 ?
   Est-il nécessaire de vérifier ces nombres ?
    

3. Continuer en donnant modulo 16 les entiers qu’il est nécessaire de vérifier.

    On pourrait continuer ainsi et démontrer qu’il n’est nécessaire de vérifier, modulo 256, que 19 nombres sur 256, soit 7,4 % de l’ensemble des nombres. Les programmeurs qui ont réussi à vérifier la conjecture pour de grandes valeurs de N ont même considéré les nombres modulo 2¹⁶ = 65536.