Nombres réels et Analyse
Fonctions - Thème N°10
Fonctions paires, fonctions impaires.
Décomposition.

    Objectif : Ce thème montre tout d’abord qu’une fonction quelconque définie sur R peut se décomposer en somme d’une fonction paire et d’une fonction impaire (question 1), puis propose deux exemples simples (question 2), une application astucieuse pour la résolution d’une équation fonctionnelle (question 3), et enfin un prolongement algorithmique (question 4).

    Niveau et difficultés :  Le thème s’adresse à l’élève de 1ère S, à l’exception de la question 3, plutôt réservée à la classe de Terminale. Rien ne va au-delà des connaissances des programmes.

1. Décomposition d'une fonction quelconque

    Soit f : R® R une fonction quelconque.

1. On définit deux fonctions de R dans R associées à f, notées respectivement f_p et f_i par :
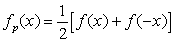   et .
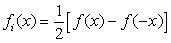   Montrer que f_p est une fonction paire et f_i est une fonction impaire.
2. Supposons qu’il existe une fonction paire g et une fonction impaire h, définies de R dans R, telles que f = g + h.
   Montrer que nécessairement et g = f_p et h = f_i.
3. Déduire des questions précédentes que toute fonction f de R dans R se décompose de manière unique en somme d’une fonction paire et d’une fonction impaire.
   Les fonctions f_p et f_i sont appelées respectivement « partie paire » et « partie impaire » de f.

2. Étude de deux cas particuliers :

a) Fonction polynomiale.

    On considère la fonction polynomiale P définie par : P(x) = 5x⁶ + 3x⁵ - 4x³ + 2x² - x + 1.
    Vérifier que la partie paire P_p et la partie impaire P_i de la fonction P sont des fonctions polynômes, que l’on exprimera.
    Quelle remarque peut-on faire sur la partie paire et sur la partie impaire d’une fonction polynôme ?

b) Fonction exponentielle.

    Dans cette question, on pose f(x) = exp(x) et l’on note respectivement ch et sh les fonctions f_p et f_i associées.

1. Calculer les dérivées ch’ et sh’ ;
2. Montrer que pour tout réel x, on a : ch²(x)-sh²(x) = 1 ;
3. Montrer que, pour tout réel x, on a :
   ch(2x) = 2ch²(x) - 1 et
   sh(2x) = 2sh(x)ch(x).

(A cause de certaines analogies frappantes dans les relations précédentes, les fonctions ch et sh sont appelées respectivement « cosinus hyperbolique » et « sinus hyperbolique ».)

3. Détermination d’une solution d’équation « fonctionnelle différentielle ».

    Soit f : R® R une fonction deux fois dérivable sur R et vérifiant pour tout réel x :
    (E)    f"(x) + f(-x) = x + x².

1. Montrer que chacune des fonctions f_p et f_i associées à f est solution d’une équation différentielle du second ordre ;
2. Déterminer une fonction polynomiale vérifiant chacune des équations différentielles précédentes.
   En déduire une solution particulière de l’équation (E).

4. Décomposition et ramification d’une fonction polynôme.

1. Montrer que pour toute fonction polynôme P peut s’écrire de manière unique sous la forme :
   P(x) = P₀(x²) + xP₁(x²), où P₀ et P₁ sont des fonctions polynômes.
   (Utiliser la question 1).
   P donne donc naissance à deux polynômes P₀ et P₁.
   De même ces deux derniers polynômes donnent respectivement P₀₀, P₀₁, P₁₀ et P₁₁ selon le schéma suivant :

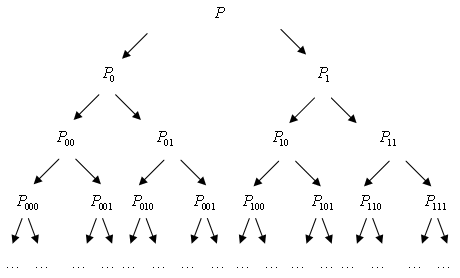
Présentation d’un exemple : avec P(x) = 5x⁶ + 3x⁵ - 4x³ + 2x² - x + 1.

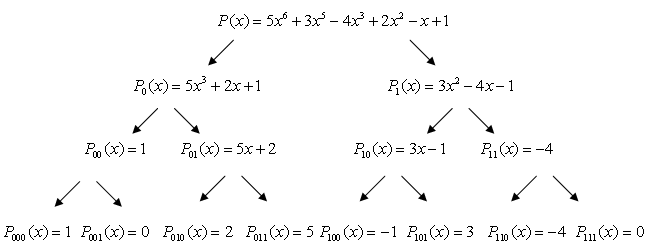
2. Inversement, existe-t-il une fonction polynôme P vérifiant les conditions :
   P₁₁₁(x) = 4 ; P₁₁₀(x) = 0 ; P₁₀₁(x) = 0 ; P₁₀₀(x) = 3 ;
   P₀₁₁(x) = 5 ; P₀₁₀(x) = 3 ; P₀₀₁(x) = -1 ; P₀₀₀(x) = 6 ?