La Chasse au trésor ! Les solutions...
mardi 11 novembre 2014

[(Première étape :)]
Décryptez le message pour trouver les quatre villes du parchemin.
Pour en savoir plus sur le code César, vous pouvez consulter ce site internet : http://www.cryptage.org/chiffre-cesar.html
Solution :
- GEVGEWWSRRI est Carcassonne avec une clé de 4.
- NZMBX est Nancy avec une clé de 25.
- QBV est Pau avec une clé de 235 ≡ 1 [26].
- ERUGHDXA est Bordeaux avec une clé de 1251≡ 3 [26].
Objectifs :
- Déchiffrer un code César mais en faisant des recherches sur papier.
(avantage de la tablette par sa taille) - Penser à la notion de « congruence » pour réussir (dans les cas de Pau et Bordeaux)
- Penser à simplifier (dans le cas de Nancy, avec un parallèle sur les nombres négatifs) les recherches.
- Division euclidienne.
Différenciation :
- La principale difficulté rencontrée par les élèves est la compréhension du Code César.
Après une lecture de la page Internet, certains pensent que le code César se fait toujours avec une clé égale à 3. - Une aide peut leur être apportée avec l’indice suivant :

Remarques diverses :
Cette partie pourrait être « complexifiée » de plusieurs façons :
- Ne pas parler du code César, mais laisser les élèves faire leur propres recherches en leur donnant un indice comme un mot connu avec son codage et sa clé par exemple.
- Ne pas donner d’adresse internet pour les recherches, mais la plupart des sites expliquant le code César mettent à disposition un traducteur dans lequel il suffit de recopier le texte et la clé pour avoir la solution (même si la clé est 1251 ou négative).
- Remplacer cette adresse par la page Wikipédia correspondant au code César :
(http://fr.wikipedia.org/wiki/Chiffrement_par_décalage)
mais elle est peut être trop fournie et trop complexe pour des élèves de 5ème.
[(Deuxième étape :)]
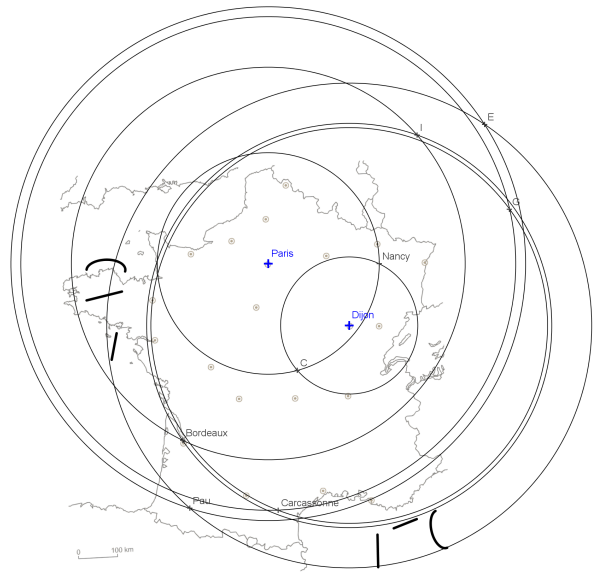
Placez avec précision ces 4 villes sur la carte papier ci-contre et trouver le centre de ces quatre villes.
Pour vous aider à placer ces villes, l’historien du navire vous conseille d’utiliser ce site : http://www.distance2villes.com/
Solution :
Pour placer les villes avec précision, les élèves doivent trouver qu’ils peuvent les placer en se servant des distances qui les séparent de Paris et Dijon qui sont sur la carte.
Ils devront pour cela chercher ces distances à vol d’oiseau sur le site internet proposé, faire des calculs d’échelles et enfin placer ces villes au compas.
Dans le cas de Nancy il y a deux possibilités, donc la consultation d’une carte sera nécessaire pour ne pas faire d’erreur.
| Paris (réelle en km) | Distance à Dijon (réelle en km) | Distance à Paris (réelle en km) | Distance à Dijon (réelle en km) | |
|---|---|---|---|---|
| Nancy | 281.71 | 174.65 | 7.04275 | 4.36625 |
| Pau | 653.73 | 616.55 | 16.34325 | 15.41375 |
| Carcassonne | 628.34 | 503.57 | 15.7085 | 1258925 |
| Bordeaux | 499.86 | 514.43 | 12.4965 | 12.86075 |
Objectifs :
- Penser au placement d’un point au compas en utilisant sa distance à deux points du plan, soin des constructions.
- Utilisation des échelles.
Différenciation :
Pour les groupes les moins à l’aise avec cette étape, on peut prévoir plusieurs indices à distribuer en fonction des besoins de chaque groupe.


Remarques diverses :
- Pour cette étape, il faut bien veiller à ce que les groupes notent les distances au fur et à mesure de leurs recherches et qu’ils pensent à se partager le travail.
- Sur la carte ci-dessus les capitales régionales sont placées avec un point.
La première classe a avoir testé l’activité avait cette carte, mais plusieurs élèves ont cru que Nancy, Carcassonne et Pau étaient certains de ces points et n’ont pas vu l’intérêt (à tort) d’utiliser les distances entre Paris, Dijon et ces villes.
Ces capitales régionales ont été retirées (à l’exception de Paris et Dijon) pour la deuxième classe, ce qui a résolu le problème. - Pour les calculs des longueurs avec l’échelle, une utilisation du tableur est envisageable.
[(Troisième étape :)]
Sur la carte de France Geogebra (qui est à la même échelle que la carte papier),
placez le plus précisément possible ces quatre villes et déterminer les coordonnées de la maison où se cache le trésor.
À l’aide du site ci-contre, trouvez le nom du village où se situe cette maison. http://www.coordonnees-gps.fr/
Solution :
Pour modifier la grille du repère, il suffit d’actionner le curseur à droite de la carte.
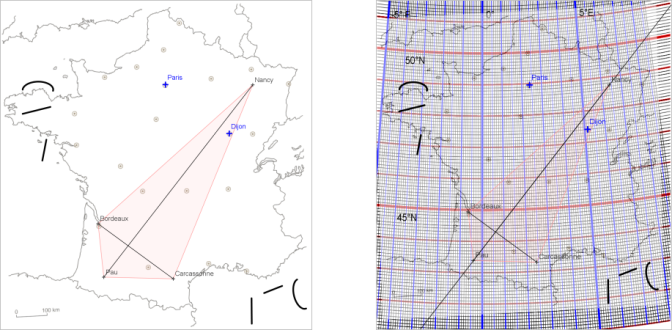
Dans le cas où les élèves ont utilisé des valeurs les plus précises possibles pour les rayons des cercles (précision au dix millième) le centre a pour coordonnées : 0,6°E et 44,3°N.
Dans le cas où ils ont arrondi au dixième ils retrouvent quasiment les mêmes coordonnées.
Le village sur lequel ils tombent avec la recherche GPS est la commune de Laugnac (village de moins de 1000 habitants).
Objectifs :
- Effectuer une construction rigoureuse sur Géogebra (constructions de cercles avec un rayon choisi, placement de points aux intersections de ces cercles, masquer certaines parties des constructions pour rendre la figure lisible…).
- Lire les coordonnées d’un point dans un repère.
Remarques diverses :
- Contrairement aux constructions de la deuxième étape, on peut utiliser des valeurs exactes pour la construction des cercles. Un débat avec les groupes peut être mené pour discuter de cette précision.
- Là encore, il n’est peut être pas nécessaire de donner l’adresse du site internet aux élèves.
Différenciation :
- Pour les groupes ayant un peu de retard, il est possible de leur fournir une carte dans laquelle une ou plusieurs villes sont déjà placées.
- On peut même envisager, pour les plus en retard, de leur fournir la carte avec les quatre villes et de les laisser construire le quadrilatère avec ses diagonales et effectuer la lecture des coordonnées.
[( Quatrième étape :)]
Vous voilà maintenant avec l’équipage dans la cave de la maison.
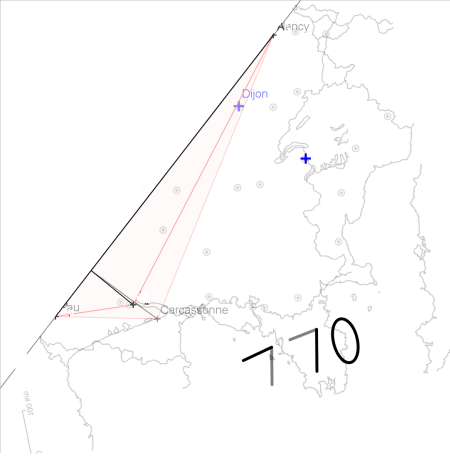
Munis de vos pelles, vous déterrez un coffre très solide avec six serrures à code et un mot dessus :

En pliant la feuille, le nombre 770 apparaît dans la mer Méditerranée.
770 peut être décomposé en 6 produits différents de trois facteurs supérieurs à 1, d’où les 6 codes.
Lorsque les élèves trouvent deux codes différents et qu’ils les rentrent dans deux cadenas de la même couleur, une partie de l’image de fin apparaît.
Pour que toute l’image apparaisse, les 6 codes doivent être trouvés
(Dans le fichier Geogebra « Trésor » l’ordre des nombres dans un code n’a en fait aucune importance et un cadenas peut accepter n’importe lequel des 6 codes, à condition qu’il ne soit pas déjà été utilisé dans un autre cadenas).
Objectif :
Décomposer un nombre en un produit de facteurs.
Les élèves trouveront assez vite les premiers codes, mais pour les derniers, une décomposition de 770 en un produit de nombres premiers (2×5×7×11) leur sera sûrement utile.
Différenciation :
Le principal problème rencontré par les groupes est la compréhension des conditions d’obtention d’un code. Pour ces groupes, on peut alors leur distribuer l’indice suivant :

Remarques diverses :
- Au début la solution souhaitée était un pliage suivant les deux axes...
mais l’épaisseur de la feuille pose alors un problème pour faire apparaître le nombre.
Tout autre pliage plus original est le bienvenu. - 770 peut être remplacé par un autre nombre pour les recherches.
- La réussite de la troisième étape étant indispensable pour aborder la quatrième étape, utiliser une information concernant la commune de Laugnac est une piste de travail pour les élèves les plus faibles.
- Une recherche sur Wikipédia permet par exemple d’avoir une étude démographique du village qui commence en 1793.
Il aurait été possible de dater le parchemin (1836 par exemple) et de dire que le nombre clés nécessaires pour trouver les codes du coffres est la population de la ville. (en 1836, il y avait 510 habitants : 510 = 2 × 3 × 5 × 17 ce qui convient pour avoir 6 codes trouvables par les élèves).

Messages
1. La Chasse au tr, 14 février 2015, 05:15, par Buford
Hi there colleagues, how is everything, and what you wish for to say regarding this piece of writing, in my view its really awesome in favor of me. My weblog cashnetusa
2. La Chasse au tr, 22 août 2015, 19:18, par Beatriz
Have you ever considered about adding a little bit more than just your articles ? I mean, what you say is important and all. However think of if you added some great graphics or videos to give your posts more, "pop" ! Your content is excellent but with images and videos, this website could certainly be one of the very best in its niche. Good blog ! Feel free to visit my web page ... quest bars